Note
Go to the end to download the full example code
Working with IBIS data
This example shows how to initialise the
mcalf.models.IBIS8542Model class with
real IBIS data, and train a neural network
classifier. We then proceed to fit the array
of spectra and visualise the results.
Download sample data
First, the sample data needs to be downloaded from the GitHub repository where it is hosted. This will create four new files in the current directory (about 651 KB total). You may need to install the requests Python package for this step to run.
Load the sample data
Next, the downloaded data needs to be loaded into Python.
# Import the packages needed for loading data
import json
import numpy as np
from astropy.io import fits
# Load the spectra's wavelength points
wavelengths = np.loadtxt('wavelengths.txt', dtype='>f4')
# Load the array of spectra
with fits.open('spectra.fits') as hdul:
spectra = hdul[0].data
# Load indices of labelled spectra
with open('training_data.json', 'r') as f:
data = f.read()
training_data = json.loads(data)
As you can see, the sample data consists of a 60 by 50 array of spectra with 27 wavelength points,
print(wavelengths.shape, spectra.shape)
(27,) (27, 60, 50)
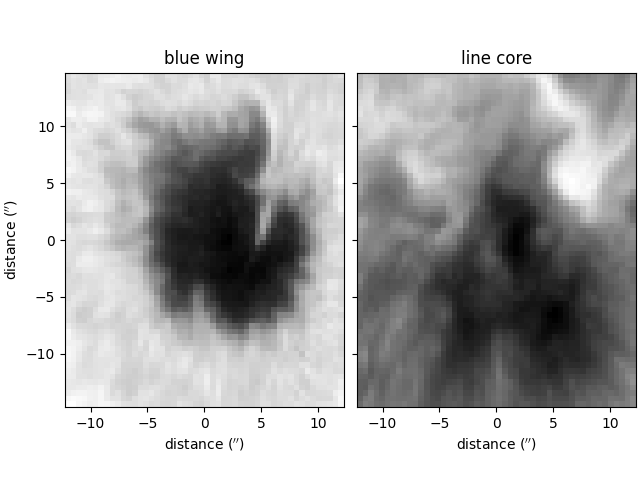
The blue wing and line core intensity values of the spectra are plotted below for illustrative purposes,
import matplotlib.pyplot as plt
import astropy.units as u
from mcalf.visualisation import plot_map
fig, ax = plt.subplots(1, 2, sharey=True, constrained_layout=True)
wing_data = np.log(spectra[0])
core_data = np.log(spectra[len(wavelengths)//2])
res = {
'offset': (-25, -30),
'resolution': (0.098 * 5 * u.arcsec, 0.098 * 5 * u.arcsec),
'show_colorbar': False,
}
wing = plot_map(wing_data, ax=ax[0], **res,
vmin=np.min(wing_data), vmax=np.max(wing_data))
core = plot_map(core_data, ax=ax[1], **res,
vmin=np.min(core_data), vmax=np.max(core_data))
wing.set_cmap('gray')
core.set_cmap('gray')
ax[0].set_title('blue wing')
ax[1].set_title('line core')
ax[1].set_ylabel('')
plt.show()
Generate the backgrounds array
As discussed in the Using IBIS8542Model example, a background intensity value must be specified for each spectrum.
For this small sample dataset, we shall simply use the average of the four leftmost intensity values of each spectrum,
backgrounds = np.mean(spectra[:4], axis=0)
Initialise the IBIS8542Model
The loaded data can now be passed into
an mcalf.models.IBIS8542Model
object.
import mcalf.models
model = mcalf.models.IBIS8542Model(original_wavelengths=wavelengths, random_state=0)
model.load_background(backgrounds, ['row', 'column'])
model.load_array(spectra, ['wavelength', 'row', 'column'])
Training the neural network
By default, the mcalf.models.IBIS8542Model
object is loaded with an untrained neural network,
The mcalf.models.IBIS8542Model
class provides two methods to train and test
the loaded neural network.
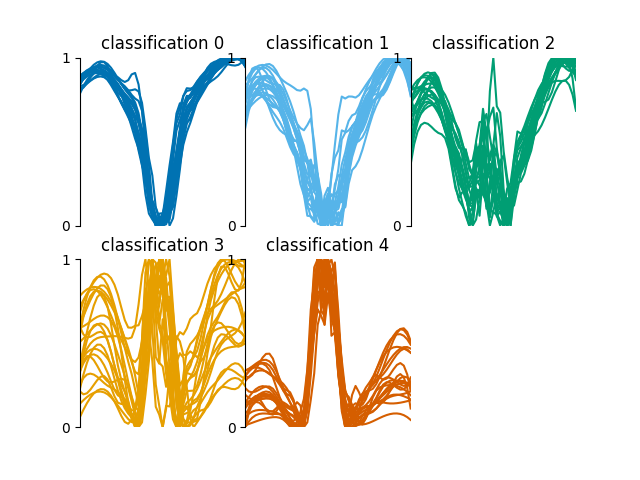
The training_data.json file contains a
dictionary of indices for each classification
0 to 5. These indices correspond to randomly
pre-chosen spectra in the spectra.fits file.
The training set consists of 200 spectra; 40 for each classification. This training set is for demonstration purposes only, generally it is not recommended to train with such a relatively high percentage of your data, as the risk of overfitting the neural network to this specific 60 by 50 array is increased.
To begin, we’ll convert the list of indices into a list of spectra and corresponding classifications,
from mcalf.utils.spec import normalise_spectrum
def select_training_set(indices, model):
for c in sorted([int(i) for i in indices.keys()]):
i = indices[str(c)]
spectra = np.array([normalise_spectrum(
model.get_spectra(row=j, column=k)[0, 0, 0],
model.constant_wavelengths, model.constant_wavelengths
) for j, k in i])
try:
_X = np.vstack((_X, spectra))
_y = np.hstack((_y, [c] * len(spectra)))
except NameError:
_X = spectra
_y = [c] * len(spectra)
return _X, _y
X, y = select_training_set(training_data, model)
print(X.shape) # spectra
print(y.shape) # labels/classifications
(200, 49)
(200,)
These classifications look as follows,
GridSpec(2, 3)
Now we can train the neural network on 100 labelled spectra (even indices),
And now we can use the other 100 labelled spectra (odd indices) to test the performance of the neural network,
+---------------------------------------------+
| Neural Network Testing Statistics |
+---------------------------------------------+
| Percentage predictions==labels :: 89.00% |
+---------------------------------------------+
| Average deviation for each classification |
+---------------------------------------------+
| class 0 :: 0.00 ± 0.00 |
+---------------------------------------------+
| class 1 :: 0.20 ± 0.68 |
+---------------------------------------------+
| class 2 :: 0.10 ± 0.44 |
+---------------------------------------------+
| class 3 :: 0.00 ± 0.32 |
+---------------------------------------------+
| class 4 :: -0.05 ± 0.22 |
+---------------------------------------------+
| Average deviation overall :: 0.05 ± 0.41 |
+---------------------------------------------+
precision recall f1-score support
0 0.95 1.00 0.98 20
1 0.94 0.80 0.86 20
2 0.89 0.80 0.84 20
3 0.75 0.90 0.82 20
4 0.95 0.95 0.95 20
accuracy 0.89 100
macro avg 0.90 0.89 0.89 100
weighted avg 0.90 0.89 0.89 100
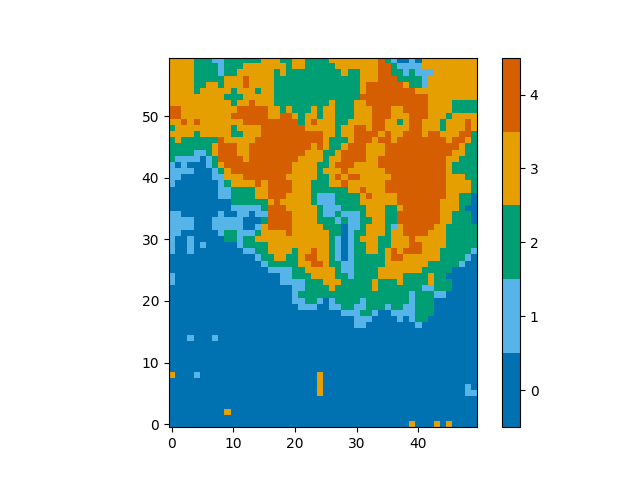
Now that we have a trained neural network, we can use it to classify spectra. Usually spectra will be classified automatically during the fitting process, however, you can request the classification by themselves,
classifications = model.classify_spectra(row=range(60), column=range(50))
These classifications look as follows,
from mcalf.visualisation import plot_class_map
plot_class_map(classifications)
<matplotlib.image.AxesImage object at 0x7f0cc7869580>
Creating a reproducible classifier
The neural network classifier introduces a certain amount of randomness when it it fitting based on the training data. This randomness arises in the initial values of the weights and biases that are fitted during the training process, as well as the order in which the training data are used.
This means that two neural networks trained on identical
data will not produce the same results. To aid the
reproducibility of results that rely on a neural
network’s classifications, a random_state integer
can be passed to mcalf.models.IBIS8542Model
as we did above. When we set this value to an integer,
no matter how many times we train the neural network
on the same data, it will always give the same
results.
Until better solutions are available to store trained neural networks, a trained neural network can be saved to a Python pickle file and later reloaded. For maximum compatibility, it is recommended to reload into the same version of scikit-learn and its dependencies.
The neural network trained above can be saved as follows,
import pickle
pkl = open('trained_neural_network.pkl', 'wb')
pickle.dump(model.neural_network, pkl)
pkl.close()
This trained neural network can then be reloaded at a later date as follows,
import pickle
pkl = open('trained_neural_network.pkl', 'rb')
model.neural_network = pickle.load(pkl) # Overwrite the default untrained model
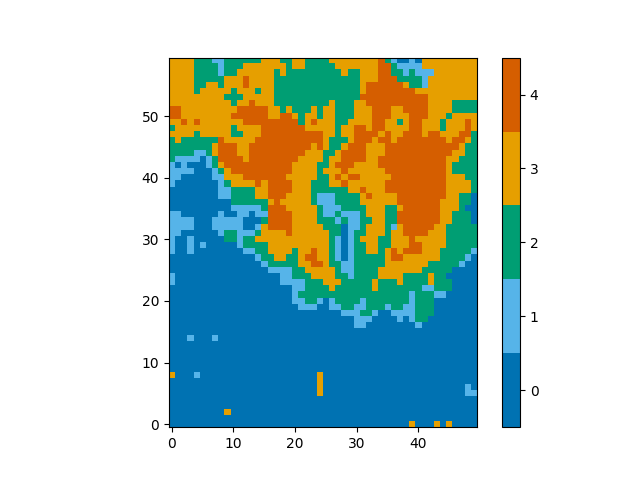
And you can see that the classifications of spectra are the same,
plot_class_map(model.classify_spectra(row=range(60), column=range(50)))
<matplotlib.image.AxesImage object at 0x7f0cc6db5280>
Please see the scikit-learn documentation for more details on model persistence.
Fitting the spectra
Now that the data have been loaded and the neural network has been trained, we can proceed to fit the spectra.
Using pre-calculated results
As our 60 by 50 array contains 3000 spectra, it would
take roughly 10 minutes to fit them all over 6 processing
pools. We include pre-calculated results in the
downloaded results.fits file.
The next step of the example loads this file back into
Python as though we have just directly calculated it.
This isn’t something you would usually need to do,
so do not worry about the contents of the
load_results() function, however, we plan to
include this functionality in MCALF itself in the future.
def load_results(file):
with fits.open(file) as hdul:
for hdu in hdul:
if hdu.name == 'PARAMETERS':
r_parameters = hdu.data.copy().reshape(-1, 8)
elif hdu.name == 'CLASSIFICATIONS':
r_classifications = hdu.data.copy().flatten()
r_profile = np.full_like(r_classifications, 'both', dtype=object)
r_profile[r_classifications <= 1] = 'absorption'
elif hdu.name == 'SUCCESS':
r_success = hdu.data.copy().flatten()
elif hdu.name == 'CHI2':
r_chi2 = hdu.data.copy().flatten()
results = []
for i in range(len(r_parameters)):
fitted_parameters = r_parameters[i]
fit_info = {
'classification': r_classifications[i],
'profile': r_profile[i],
'success': r_success[i],
'chi2': r_chi2[i],
'index': [0, *np.unravel_index(i, (60, 50))],
}
if fit_info['profile'] == 'absorption':
fitted_parameters = fitted_parameters[:4]
results.append(mcalf.models.FitResult(fitted_parameters, fit_info))
return results
result_list = load_results('results.fits')
result_list[:4] # The first four
[Successful FitResult at (0, 0, 0) with absorption profile of classification 0, Successful FitResult at (0, 0, 1) with absorption profile of classification 0, Successful FitResult at (0, 0, 2) with absorption profile of classification 0, Successful FitResult at (0, 0, 3) with absorption profile of classification 0]
Using your own results
You can run the following code to generate
the result_list variable for yourself.
Try starting with a smaller range of rows
and columns, and set the number of pools
based on the specification of your
processor.
# result_list = model.fit(row=range(60), column=range(50), n_pools=6)
The order of the mcalf.models.FitResult
objects in this list will also differ as
the order that spectra finish fitting in
each pool is unpredictable.
Merging the FitResult objects
The list of mcalf.models.FitResult
objects can be mergerd into a
mcalf.models.FitResults object,
and then saved to a file, just like the
results.fits file downloaded earlier.
First the object needs to be initialised with the spatial dimensions and number of fitted parameters,
results = mcalf.models.FitResults((60, 50), 8)
Now we can loop through the list of fits and append them to this object,
for fit in result_list:
results.append(fit)
This object can then be saved to file,
results.save('ibis8542data.fits', model)
The file has the following structure,
Filename: ibis8542data.fits
No. Name Ver Type Cards Dimensions Format
0 PRIMARY 1 PrimaryHDU 13 (0,)
1 PARAMETERS 1 ImageHDU 12 (8, 50, 60) float64
2 CLASSIFICATIONS 1 ImageHDU 10 (50, 60) int16
3 PROFILE 1 ImageHDU 11 (50, 60) int16
4 SUCCESS 1 ImageHDU 10 (50, 60) int16
5 CHI2 1 ImageHDU 10 (50, 60) float64
6 VLOSA 1 ImageHDU 12 (50, 60) float64
7 VLOSQ 1 ImageHDU 12 (50, 60) float64
Exploring the fitted data
You can plot a fitted spectrum as follows,
model.plot(result_list[0])
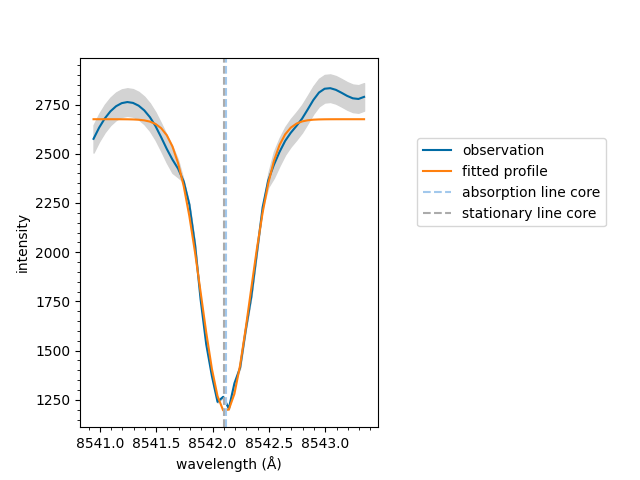
<Axes: xlabel='wavelength (Å)', ylabel='intensity'>
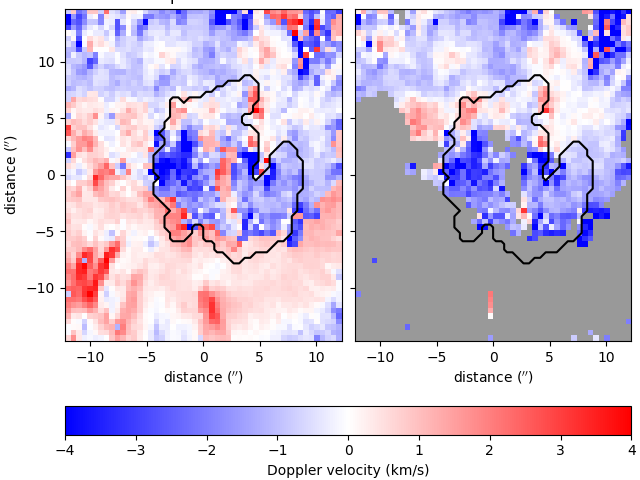
You can calculate and plot Doppler velocities for both the quiescent and active regimes as follows, (with an outline of the sunspot’s umbra),
vq = results.velocities(model, vtype='quiescent')
va = results.velocities(model, vtype='active')
umbra_mask = np.full_like(backgrounds, True)
umbra_mask[backgrounds < 1100] = False
fig, ax = plt.subplots(1, 2, sharey=True, constrained_layout=True)
settings = {
'show_colorbar': False, 'vmax': 4, 'offset': (-25, -30),
'resolution': (0.098 * 5 * u.arcsec, 0.098 * 5 * u.arcsec),
'umbra_mask': umbra_mask,
}
im = plot_map(vq, ax=ax[0], **settings)
plot_map(va, ax=ax[1], **settings)
ax[0].set_title('quiescent')
ax[1].set_title('active')
ax[1].set_ylabel('')
fig.colorbar(im, ax=ax, location='bottom', label='Doppler velocity (km/s)')
plt.show()
Total running time of the script: ( 0 minutes 8.174 seconds)